In diesem Beispiel soll gezeigt werden wie einfach mittels HTflux thermische Kennwerte auch von inhomogenen Bauteilen, wie sie uns etwa oft im Holzbau begegnen, präzise bestimmt werden können. Neben dem U-Wert (Wärmedurchgangskoeffizient) werden auch die dynamischen thermischen Kenngrößen des Aufbaus ermittelt.

Das Modell

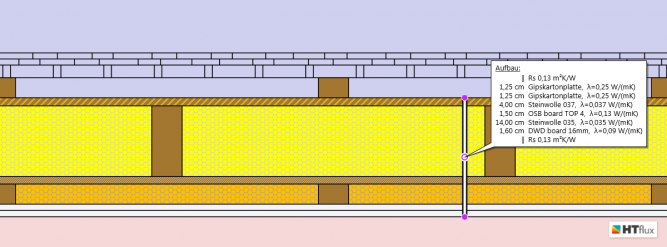
Untersucht wird eine klassische Holzrahmenkonstruktion, wie sie im sogenannten „Holzleichtbau“ eingesetzt wird.

Die Dämmung erfolgt hierbei hauptsächlich über Mineralwolle (60 cm), welche zwischen den Holzständern (6 cm) eingebracht wird. Zur Versteifung sind innen und außen Holzwerkstoffplatten angebracht. (Anm. um Kondensation zu vermeiden ist darauf zu achten, dass die innenliegende Platte einen höheren Diffusionswiderstand als die äußere aufweist – siehe unten). Der „Innenausbau“ besteht klassisch aus doppelter Gipskartonbeplankung auf Holzlattung. Außen wurde eine Schindelfassade angedeutet, da laut Norm die thermische Simulation nur bis zur Hinterlüftungsebene zu erfolgen hat, könnte es sich hierbei jedoch um eine beliebige Fassade handeln.

Dynamisch-thermische Kenngrößen (gemäß EN ISO 13786)

HTflux ermöglicht es sehr einfach die Wärmeaufnahme Y₁₁, dynamische Wärmeaufnahme Y₁₂ und flächenbezogene wirksame Wärmekapazität χ samt zeitlichen Phasenverschiebungen, wie in EN ISO 13786 definiert, zu ermitteln.
Diese spielen derzeit hauptsächlich bei der Vermeidung von sommerlicher Überhitzung eine Rolle und werden von den einschlägigen Normen gefordert. Sie können aber auch für die Beurteilung und Optimierung von weiteren Anwendungsfällen eingesetzt werden. Denn Kennwerten kommt derzeit auch wachsendes Interesse zu, da es mit einer entsprechenden Optimierung möglich ist die Energieeffizienz von Gebäuden zu steigern.

Vergleich analytische Berechnung („1d“) und zweidimensionale Simulation („2d“)

Sowohl für den U-Wert, als auch für die dynamischen Kenngrößen können die Werte in der Regel (d.h. unter der Einhaltung bestimmter Bedingungen) auch für inhomogene Bauteile mittels vereinfachter Verfahren analytisch (also ohne Simulation) berechnet werden. Beim U-Wert erfolgt diese Abschätzung durch Mittelung des minimal- und maximal-möglichen Wärmestroms. Bei den dynamischen Kennwerten werden üblicherweise die durchdringenden Elemente, wie Holzbalken, ganz vernachlässigt. Grundsätzlich weisen die entsprechenden Normen (z.B. EN ISO 6946 und EN ISO 13786) jedoch immer darauf hin, dass eine entsprechende Simulation zu exakteren Ergebnissen führt, und die Verwendung dieser natürlich zulässig ist.

Je nach Aufbau der Bauteile können die Unterschiede zwischen vereinfachter Berechnung („1d“) und Ermittlung aus thermischer Simulation entweder signifikant oder vernachlässigbar sein. Grundsätzlich sind die Unterschiede natürlich markanter wenn die Wärmeleitfähigkeiten der beteiligten Materialen stark unterschiedlich sind (z.B. Dämmstoffe zwischen Beton- oder Stahlteilen). Im vorliegenden Beispiel sind die Unterschiede eher gering, da die Wärmeleitfähigkeit der Holzelemente im Vergleich zu anderen Baustoffen niedrig ist und damit näher bei jenem des verwendeten Dämmstoffs liegt.

U-Wert-Ermittlung (Wärmedurchgangskoeffizient)

In HTflux kann mittels vier Maus-Clicks das U-Wert Tool zur exakten Berechnung des U-Werts angewendet werden. Hierbei ist lediglich darauf zu achten, dass zur Berechnung exakt ein oder mehrere Abschnitte gewählt werden, welche der Breite des sich wiederholenden Aufbaus entsprechen (hier 66 cm). Nach Aufruf der Simulation, welche nur Sekunden dauert, können eine Vielzahl von Werten zur thermischen Charakterisierung des Bauteils angezeigt werden.

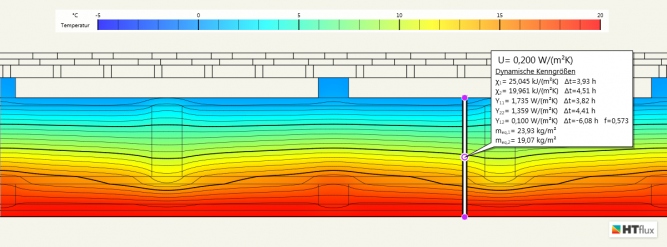
Im Beispiel wird ein U-Wert von 0,200 W/mK ermittelt. Eine entsprechende Berechnung nach dem vereinfachten Verfahren für inhomogene Schichten (gemäß EN ISO 6946) ergibt einen Wert von 0,202 W/mK. Die vereinfachte Berechnung liefert somit in diesem Fall einen guten Näherungswert, der nur um 1% über dem tatsächlichen Wert liegt. Die Gründe für die geringe Abweichung wurden bereits oben erläutert.

Dynamisch thermische Kenngrößen

Wie in der Temperaturansicht zu sehen ist, liefert das angewendete U-Wert Tool auch bereits die dynamisch thermischen Kenngrößen nach dem vereinfachten Verfahren mit. Diese Werte werden nach dem in der Norm beschriebenen Verfahren unter der Annahme von homogenen, unendlich ausgedehnten Materialebenen berechnet, und können damit den Einfluss von Lattung und Holzriegel nicht abbilden.  Um zu überprüfen, wie stark die so ermittelten Werte von den tatsächlichen Werten abweichen, wird eine transiente (=zeitaufgelöste) thermische Simulation mit HTflux durchgeführt. Hierbei werden die inneren und äußeren Temperaturen mit einer Periode von 24 Stunden variiert und die daraus resultierenden Wärmestromverläufe an der Innen- und Außenseite gemessen.

Durch Quotientenbildung von Temperatur- und Wärmestromamplitude kann die flächenbezogene wirksame Wärmekapazität χ entsprechend der Norm-Definition direkt ermittelt werden.

Im Vergleich zeigt sich, dass die Wärmekapazität innen 4% über jener aus der vereinfachten Berechnung liegt. Die Erhöhung resultiert aus dem Einfluss der Holzlattung, welche im vereinfachten Verfahren nicht berücksichtigt wird. Die relativ geringe Abweichung mag überraschen, erklärt sich aber durch die geringe periodische Eindringtiefe des Wärmestroms. Dies bedeutet, dass eine signifikante Wärmespeicherung praktisch nur im Bereich der Gipskartonplatten stattfindet.

Anmerkung: bei dieser Berechnung wurden die Wärmeübergangswiderstände innen mit 0,13 W/mK angenommen, wird – wie in manchen nationalen Normen gefordert – der Wärme­übergangs­widerstand vernachlässigt, so ergeben sich einerseits höhere Werte und andererseits eine größere Abweichung zur vereinfachten Berechnung. Die Vernachlässigung der Wärmeübergangswiderstände ist jedoch physikalisch nicht plausibel.

Außenseitig ist die Abweichung zwischen vereinfachter Berechnung und exakter Simulation mit 17% deutlich signifikanter.  Dies erklärt sich daraus, dass ein größerer Teil des Wärmestroms über die leichte Holzwerkstoffplatte bis zu den massiven Holzständer vordringen kann und damit dessen Wärmekapazitäten zusätzlich „genutzt“ werden können. Auf den Temperaturverlauf im Innenraum hat dieser Effekt jedoch praktisch keinen Einfluss.

Quasi nebenbei entstehen bei der Simulation auch Videos, welche die Temperaturschwankungen und Wärmestromverläufe sehr gut wahrnehmbar machen:

Wärmestrom bei periodischem Temperaturverlauf als Video:

Temperaturverteilung bei periodischem Temperaturverlauf als Video:

Vergleichstabelle: vereinfachte Berechnung / Simulation

Die Ergebnisse der vereinfachten Berechnung („1d“) im Vergleich mit den genaueren Ergebnissen der zeitaufgelösten thermischen Simulation:

Wie bereits erwähnt, sind die Unterschiede bei diesem Beispiel aus den oben genannten Gründen eher gering. Bei anderen inhomogenen Bauteilaufbauten können die Unterschiede signifikanter ausfallen, insbesondere wenn Materialien mit hoher Wärmeleitfähigkeit beteiligt sind.

Anhang – Wasserdampfdiffusion / Glaser 2d

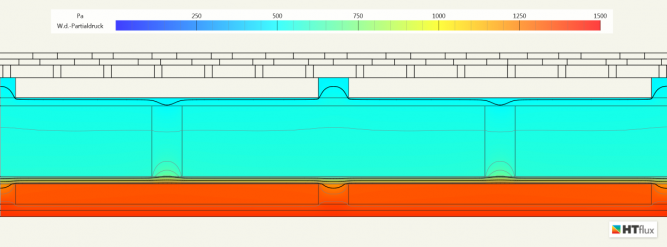
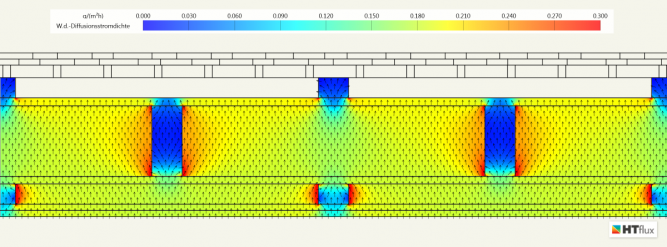
Auch dieses Beispiel eignet sich gut dazu darauf hinzuweisen, dass mittels HTflux quasi ohne zusätzlichen Aufwand eine detaillierte Untersuchung der Wasserdampfdiffusion und der damit einhergehenden Kondensationsgefahr durchgeführt werden kann.

Die Glaser 2d-Simulation zeigt, dass bei dieser Konstruktion unter den angenommenen Randbedingungen mit keiner Kondensatbildung zu rechnen ist.

 

Autor: DI Daniel Rüdisser, HTflux

 Anmerkung: Wir erlauben und begrüßen ausdrücklich die Verwendung des Bildmaterials auf dieser Seite und die Setzung von Links zu dieser Seite, sofern als Quelle „www.htflux.com“ angegeben wird.